오늘은 Feedback Contoller를 설계하는 방법에 대해서 한번 정리하는 시간을 가져 보도록 하겠습니다.
Feedback이라는 것은 무언가를 되먹인다는 뜻입니다.
되먹인다는 것이 무엇이고,
Feedback Controller 제어 방법에는 어떤것이 있을까요?
한번 알아보도록 하겠습니다.
참고리 이 글은 제어에 관하여 연재를 하고 있는 글들입니다.
이전 글들을 참고해 주세요!!
1) 제어란 무엇인가?
https://embeddedchallenge.tistory.com/475
2) 매트랩이란? 매트랩 학생용 다운로드 및 라이센스 받는 방법
https://embeddedchallenge.tistory.com/477
3) 매트랩 기초 연습 (행렬 연산, 데이터 나누기, 그래프 그리기)
https://embeddedchallenge.tistory.com/478
4) 지수함수, 모터 모델링, 전달함수, 시간함수 정리
https://embeddedchallenge.tistory.com/479
5) DC모터 모델링, 매트랩 전달함수 생성 후 그래프 확인
https://embeddedchallenge.tistory.com/480
6) Simulink를 이용한 전달함수 시뮬레이션 수행 방법 정리
https://embeddedchallenge.tistory.com/481
7) DAQ? Data Acquisition? DC모터 전달함수의 K와 Tau 값을 계산, 확인하는 방법 정리
https://embeddedchallenge.tistory.com/482
그전에 바로 전 글에서 DC모터 응답 특성을 시뮬레이션 했는데
그 응답특성을 한번 생각해 보도록 하겠습니다.
우리가 제어의 관점에서 응답특성을 볼때
크게 3가지를 point를 주목합니다.
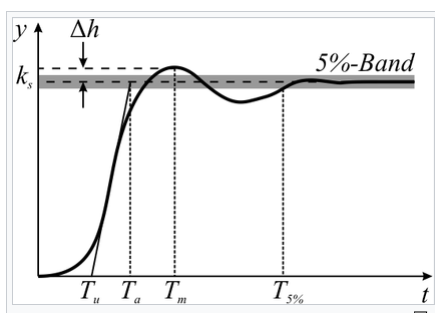
1) Rising Time : 응답되는 값이 10%~ 90% 까지 변하는 시간
Rising Time이 빠를수록 목표값에 더 빨리 도달되는 것을 확인 할수 있습니다.
2) Settling Time : 목표값과의 오차가 2% 또는 5% 이내로 들어오는 시점을 의미합니다.
결국 최종 목표값에 근사하게 도달하는 시간을 의미합니다.
3) OverShoot : 아래 그림에서 볼록 튀어오른 부분이 보입니다.
즉 Peak 값과 수렴값의 차이를 %로 나타낸 것을 의미합니다.
그렇다면 우리가 만든 모델의 응답시간을 확인하기 위해서 아래 코드를 한번 돌려보겠습니다.
우선 아래가 우리가 만든 모델입니다.
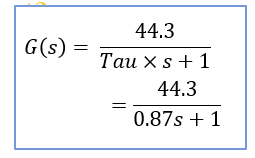
이것을 아래와 같이 넣고 돌리겠습니다.
그리고 stepinfo를 돌려보도록 하겠습니다.
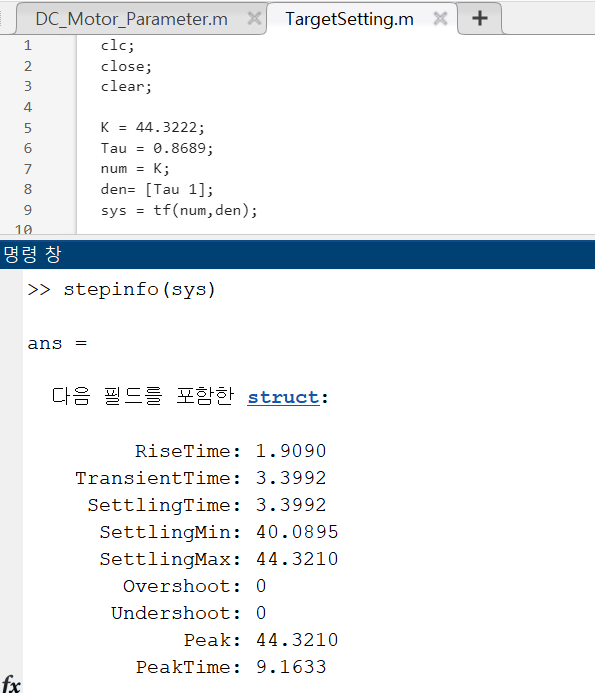
그렇다면 Rising TTime : 1.9090
Settling Time : 3.39s 가 나오고 있는것을 볼수 있습니다.
그림으로 그리면 아래와 같습니다.

Rising Time이 1.9초가 걸린다는 것은
DC모터로 자동차를 만든다고 할때 응답속도가 많이 느려 보입니다.
이제 목표 응답특성을 한번 제시해 보겠습니다.
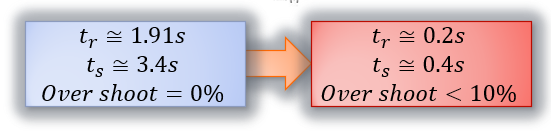
Rising Time을 0.2초 이내로
Settling Time을 0.4초 이내로
단, Overshoot는 10%미만으로 모터의 응답속도를 개선해 보겠습니다.
바로 'Feedback'제어기를 만들어서 말입니다.
제어기를 만드는 방법은 여러가지 방법이 있습니다.
우선, Feedback Contoller를 한번 설계해 보도록 하겠습니다.
그리고 Feedback Controller 방법 중에서 PID 제어기를 한번 설계해 보도록 하겠습니다.
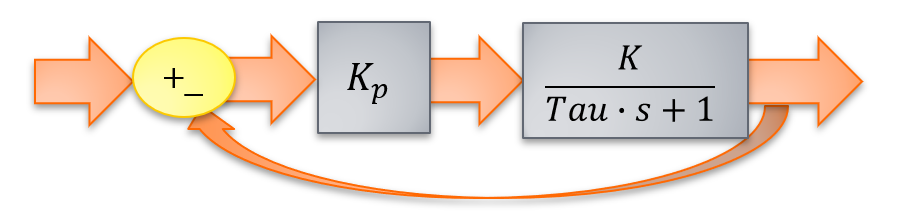
아래가 Feedback Controller의 모습입니다.
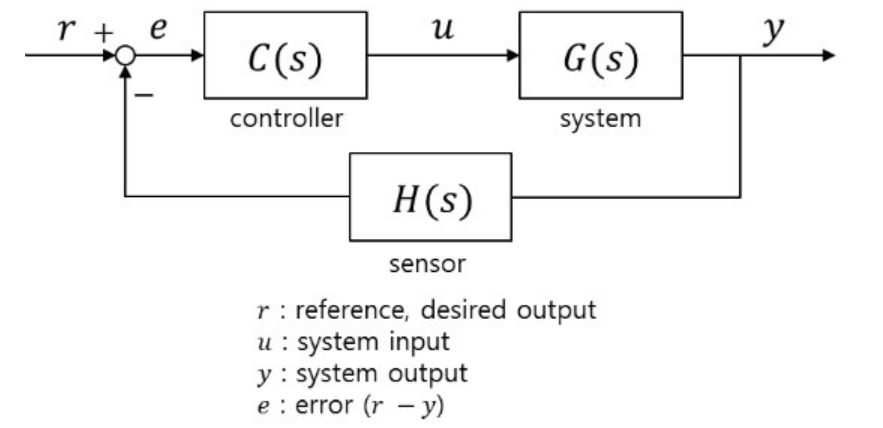
즉, Sensor를 이용하여
r은 목표값입니다.
예를 들어 RPM 200 이라고 가정해 보겠습니다.
즉 저는 모터를 계속 200 RPM으로 유지하고 싶은 것입니다.
y는 실제 모터가 도는 RPM입니다.
그리고 H(s)는 Sensor를 통해서 그 값을 계측한 값이라고 생각하시면 됩니다.
그리고 r- 계측값 = error 가 됩니다.
그리고 그 Error값이 Contoller로 들어가게 됩니다.
Controller를 통해서 나온 u는 제어를 수행하기 위한 출력값입니다.
우리는 PWM Duty값이 될것입니다.
그리고 이것이 System(motor)로 들어가게 됩니다.
결국 모터는 RPM을 만들어 내게 되는 것이죠!
그런데 우리는 아래 빨갱색 박스를 하나의 전달함수로 만들 수 있습니다.
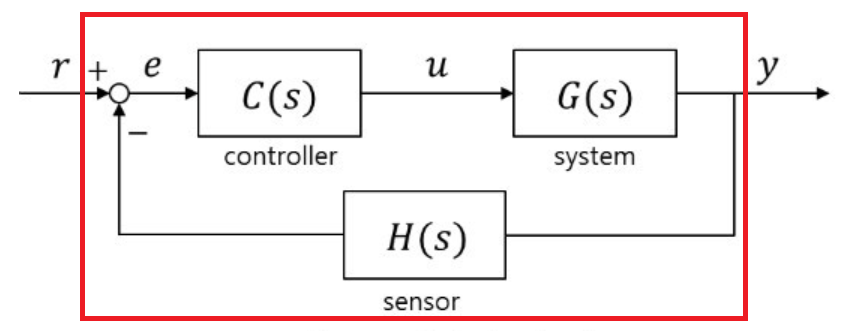
빨강박스를 전달함수를 하나로 만들면 아래와 같습니다.
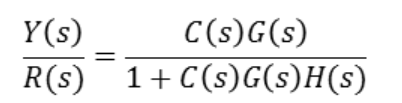
어떻게 이것이 가능한지 한번 알아 보도록 하겠습니다.
먼저 Error 부분을 보면
R(s)에서 Y(s)H(s)를 뺀것을 의미합니다.
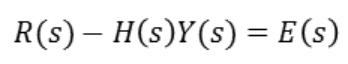
그리고 또 아래와 같이 전달함수 수식을 만들 수 있습니다.

이제 E(s)를 치환해서 넣어 보도록 하겠습니다.
아래와 같은 수식이 나오게 됩니다.
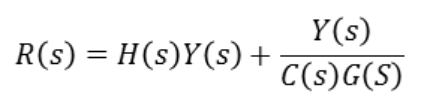
이 수식을 아래와 같이 정리할 수 있습니다.
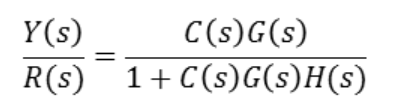
그렇다면 Feedback 제어기로 중
그렇다면 이제 Feedback 제어기 중에
PID controller를 한번 설계해 보도록 하겠습니다.
PID의 약어는 아래와 같습니다.
PID controller : Proportional-Integral-Derivative controller
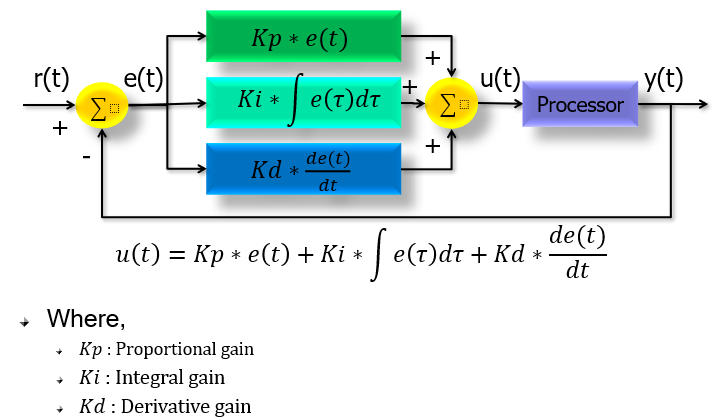
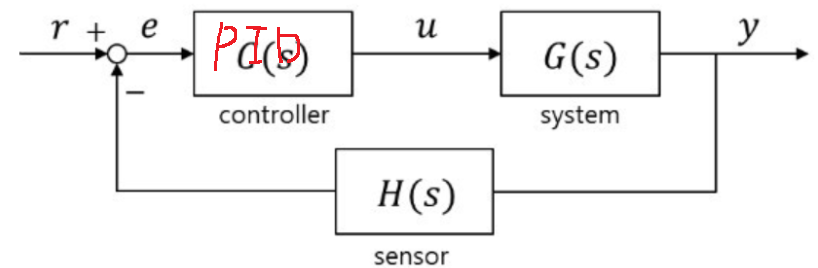
위에 그림에서 보이시나요?
C(s)라는 Controller라는 부분에 PID 제어기가 들어가 있습니다.
그리고 PID는 무조건 PID를 사용하지 않아도 됩니다.
P 제어기
PI제어기
PID 제어기
등등 제어기에 원하는 속성을 추가하여 설계하기도 합니다.
여기서 먼저 P Controller만 사용해 보도록 하겠습니다.
그리고 한번 전달함수를 만들어 보도록 하겠습니다.
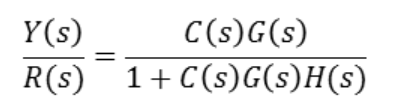
그렇다면 전달함수는 아래와 같이 됩니다.

한번 생각해 보겠습니다.
원래는 이렇게 생겼고
Pole이 아래와 같이 생겼습니다.
여기서 Pole이라는 것은
Tau*s + 1 = 0
Tau*s = -1
s = -1/Taue
즉 아래 분모의 값을 0으로 만들어주는 S값을 의미합니다.

그런데 아래와 같이 생긴 Feedback Contoller가 생성이 되고
이것의 전달함수는 위에서 증명한것 처럼 아래와 같이 변하게 되고
pole은 왼쪽으로 더 멀어지게 만들것입니다.
Tau*s = -(KpK+1)
s - -(KpK+1)/Tau
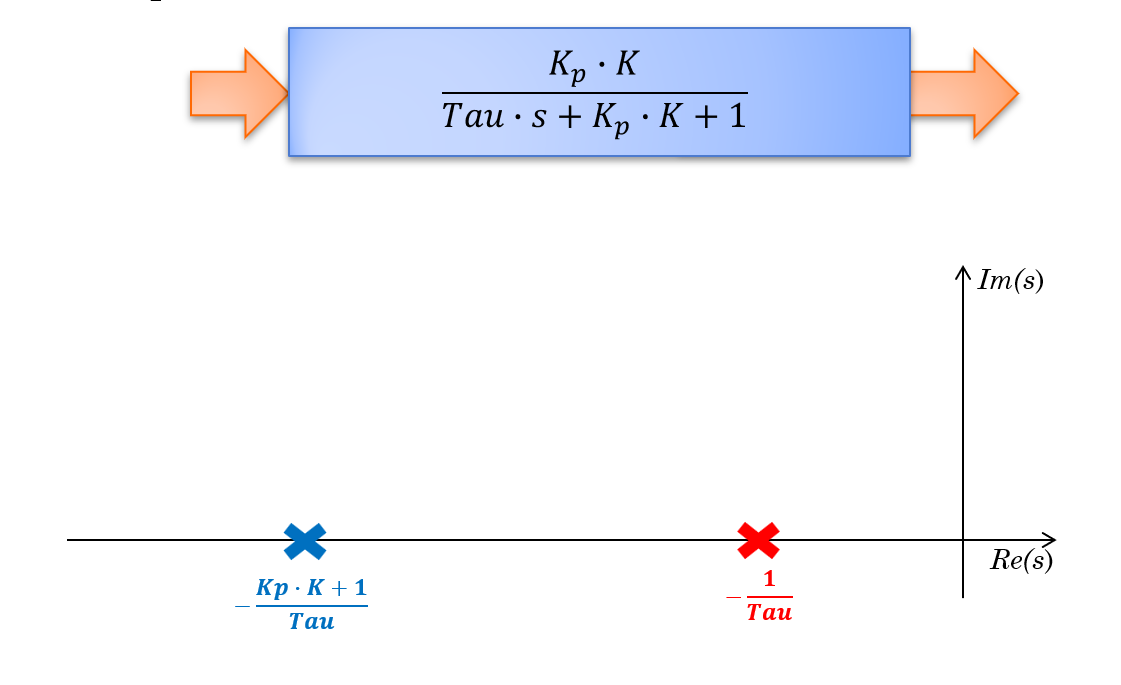
Pole이 왼쪽으로 멀어지게 되면 응답특성은 더 빨라지게 됩니다.
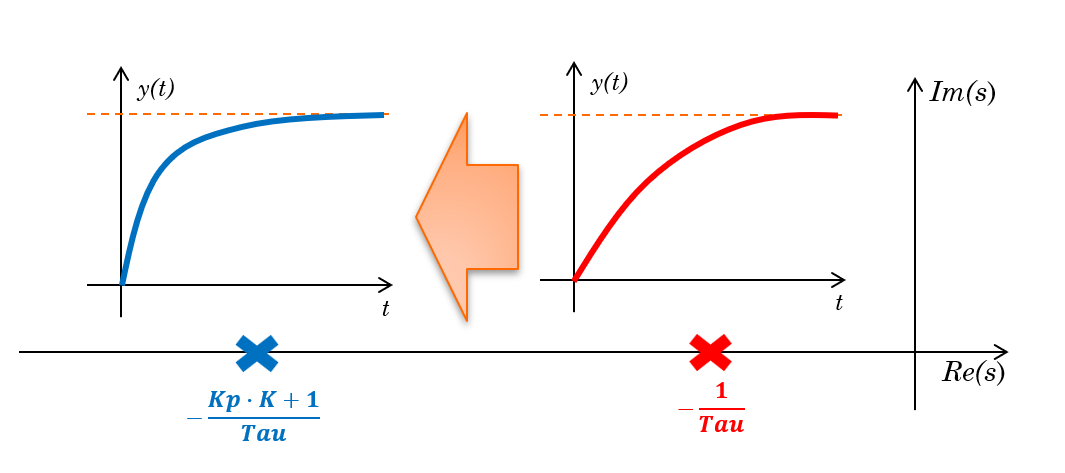
따라서 P Controller는 응답속도를 빠르게 만드는 효과를 얻을 수 있습니다.
목표치에 더 빨리 도달할 것입니다.
왜? 극점이 왼쪽에서 더 멀리 있으면 더 응답속도가 빨라지게 될까요?
우리는 벌써 이 이유에 대해서 알고 있습니다.
다음 글에서 Pole(극점)과 응답특성에 대해서 한번 알아보는 시간을 가져보도록 하겠습니다.
'Embedded SW > Control Theory' 카테고리의 다른 글
| P controller 정상오차 분석 정리 (DC모터 P 제어기 Steady State Error 분석) (0) | 2022.10.01 |
|---|---|
| Pole이란 무엇이고, 1차 전달함수에서 Pole에 위치에 따른 응답특성은? (0) | 2022.09.26 |
| DC모터 모델링 관련 매트랩 코드 정리 및 DC모터 Simulink 시뮬레이션 결과 비교 (0) | 2022.09.24 |
| DAQ? Data Acquisition? DC모터 전달함수의 K와 Tau 값을 계산, 확인하는 방법 정리 (0) | 2022.09.24 |
| Simulink를 이용한 전달함수 시뮬레이션 수행 방법 정리 (0) | 2022.09.22 |




댓글