안녕하세요.
이전시간에 P제어기를 설계하였는데
우리가 목표한 RPM이 결과로 도출되지 않고
정상오차(Steady State Error)가 발생하는 것을 확인하였습니다.
따라서 오늘은 P 제어기의 정상상태 오차를 수식으로 증명하고
결과에 맞는 값이 나오는지 알아 보도록 하겠습니다.
우선 이글을 잘 이해하기 위해서는 아래글을 먼저 읽고 오시면 좋을 것 같습니다.
(이글은 연재되고 있는 글입니다.)
1) 제어란 무엇인가?
https://embeddedchallenge.tistory.com/475
2) 매트랩이란? 매트랩 학생용 다운로드 및 라이센스 받는 방법
https://embeddedchallenge.tistory.com/477
3) 매트랩 기초 연습 (행렬 연산, 데이터 나누기, 그래프 그리기)
https://embeddedchallenge.tistory.com/478
4) 지수함수, 모터 모델링, 전달함수, 시간함수 정리
https://embeddedchallenge.tistory.com/479
5) DC모터 모델링, 매트랩 전달함수 생성 후 그래프 확인
https://embeddedchallenge.tistory.com/480
6) Simulink를 이용한 전달함수 시뮬레이션 수행 방법 정리
https://embeddedchallenge.tistory.com/481
7) DAQ? Data Acquisition? DC모터 전달함수의 K와 Tau 값을 계산, 확인하는 방법 정리
https://embeddedchallenge.tistory.com/482
8) Feedback Controller 설계 방법 정리 (ex DC모터 제어, P Controller)
https://embeddedchallenge.tistory.com/484
9) Pole이란 무엇이고, 1차 전달함수에서 Pole에 위치에 따른 응답특성은?
https://embeddedchallenge.tistory.com/485
그러면 다시 진도를 나가 보도록 하겠습니다.
우리는 이전시간에서
DC모터를 모델링하고
그 수식화된 모델링을 이용하여
P Controller를 설계해 보았습니다.
그리고 응답속도를 개선하였습니다.
Steady State Error가 발생하고 있음을 알 수 있었습니다.
Steady State 는 정상상태를 의미합니다.
시간이 많이 지난후에
우리가 목표한 값에 도달하지 않음을 알 수 있습니다.
바로 아래 그래프를 한번 살펴봐주세요.
빨강색 그래프는 Duty를 2%증가하였을때 모터의 RPM 속도 입니다.
G(s)가 모터의 특성을 나타내고 있는 전달함수를 의미합니다.
u(t)는 PWM Duty값을 72% -> 74%로 변경하여
Step으로 변하는 DC 모터 Input Voltage전압을 의미합니다.
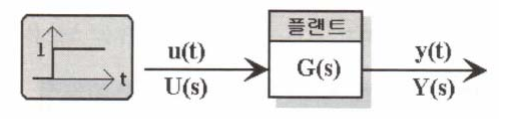
이러한 경우 아래와 같은 빨강색 그래프가 그려지고 있습니다.

그리고 파랑색은 P Controller를 설계하여 목표값을 주었습니다.
아래와 같이 제어기라고 빨강색 박스를 친것이 보이시나요?
이것은 PID 제어기 입니다.
여기서 저는 P 제어기만 사용하였습니다.
그리고 Input 값은 126RPM -> 215RPM으로 지령 RPM을 제어기로 주었습니다.

조금더 쉽게 그림을 그리면 아래와 같은 그림입니다.
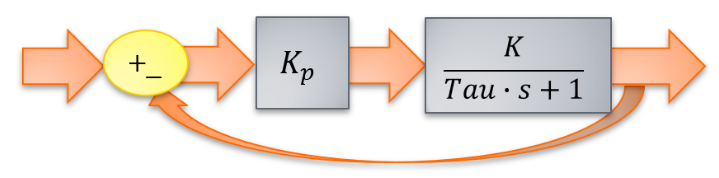
그런데 위와 같이 RPM이 215RPM에 수렴되지 못하는 것을 볼 수 있습니다.

아래 공식을 통해서 어떻게 변해가는지 알아 보도록 하겠습니다.

여기서 E(s)는 아래와 같은 수식을 가지게 됩니다.

그리고 Y(s) = E(s)C(s)G(s) 입니다.

R(s) - H(s)E(s)C(s)G(s) = E(s)
H(s) = 1
R(s) = E(s)C(s)G(s) + E(s)
E(s) = R(s)/(C(s)G(s) + 1)
E(s) = R(s) / (KpG(s) + 1)
이러한 수식으로 정리가 될 수 있습니다.
단위함수 응답이므로
R(s) = 1/s 입니다.
따라서 시간단위 e(t)를 전달함수로 변하면 아래와 같은 수식이 되기 때문에

최종 수식은
sE(s) = s*(1/s) / (Kp * G(s) + 1)
지금 실제 그래프에서 나는 오차는 아래와 같습니다.
215- 193.2 = 21.8
그러면 이제 우리가 구한 아래 수식을 통해서
정말 21.8 RPM의 오차가 나오는지 알아 보돌고 하겠습니다.

그런데, 저는 단위 응답을 주지 않았습니다.
126 -> 215의 응답을 주었기 때문의 위의 수식에서
215 / (Kp*K + 1)이 정상상태 오차가 됩니다.
이유는 R(s)최종 상태 값은 215이기 때문입니다.
그러면 수식을 한번 구해볼게요.
우리는 이전시간이
Kp = 0.2 (P gain)
K = 44.322 -> 모터모델링 파라미터
를 구했습니다.
215/(0.2*44.3222 + 1) = 215/9.86 = 21.8 RPM의 오차가 나오게 됩니다.
보이시나요?
215 - 193.2 - 21.8 입니다 ㅎㅎㅎ
정말 정확하게 설계한데로 오차가 나오고 있는것을 볼 수 있습니다.

다음에는 아래와 같이 PI 제어기를 설계하여
이러한 오차를 줄이는 방법에 대해서 정리해 보돌고 하겠습니다.
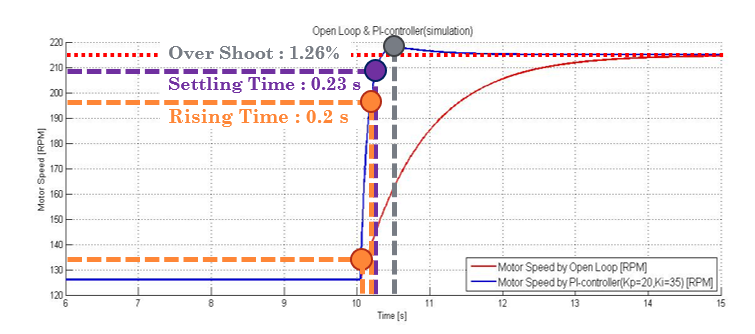
아래는 최종 결과 입니다.
우리가 PI제어기를 설계하였을때
우리는 정상상태 Error 0
그리고 아래와 같이 응답성능의 개선을 확보 할 수 있습니다.

개발을 하면서 느끼는 것은
정확한 수식 증명과 예측이 필요하다는 것입니다.
따라서 수학적인 수식정명을 꼭 하시면서
정확한 예측에 따른 실험결과가 나오는지를 항상 유념하시면서
개발하시면 좋을것 같습니다.
'Embedded SW > Control Theory' 카테고리의 다른 글
| Feedback Controller 설계 (매트랩 m파일을 이용한 시뮬레이션) (1) | 2022.10.07 |
|---|---|
| PI 제어기 설계 (PI Controller DC Motor Design) (0) | 2022.10.01 |
| Pole이란 무엇이고, 1차 전달함수에서 Pole에 위치에 따른 응답특성은? (0) | 2022.09.26 |
| Feedback Controller 설계 방법 정리 (ex DC모터 제어, P Controller) (0) | 2022.09.26 |
| DC모터 모델링 관련 매트랩 코드 정리 및 DC모터 Simulink 시뮬레이션 결과 비교 (0) | 2022.09.24 |




댓글