우리는 지금까지
DC모터에 대한 미분방정식을 만들고
1차 전달함수를 모델링하였습니다.
그리고 그 전달함수의 파라미터를 찾았습니다.
지금은 그 전달함수 파라미터를 찾는 과정에서
조금만 더 부연설명을 하고,
매트랩 활용부분에 대해서 추가 정리하는 시간을 가지도록 하겠습니다.
테스트를 통해서 저는 아래와 같은
Duty와 RPM의 관계를 획득하게 되었습니다.
| Duty (%) | 모터 속도 (RPM) |
| 72 | 110 |
| 73 | 170 |
| 74 | 210 |
| 75 | 260 |
110~ 260 RPM이 DC 모터를 제어하는데 있어서 가장 많이 사용하는 영역입니다.
따라서 이 부분에 대한 모델링을 수행하였습니다.
그리고, 저는 Duty 72 -> 74로 변경을 하여
110 -> 210 RPM으로 Step으로 속도변경을 시켰습니다.
따라서, 파랑색이 실제 모터 응답을 나타내고 있지만
빨강색으로 선형화 시켜서 모델을 만들었습니다.
clear;
clc
Duty_ratio=[72 73 74 75];
R_RPM=[110 170 210 260];
plot(Duty_ratio,R_RPM,'-o');
title('The relation between Motor speed and PWM Duty');
xlabel('Duty Ratio [%]');
ylabel('Motor Speed [RPM]');
hold on;
grid on;
TEST_X=[72 74];
TEST_Y=[110 210];
plot(TEST_X,TEST_Y,'-o');모델을 만들때, 다양한 조건을 고려할수록 모델은 복잡해 지게 됩니다.
따라서, 우선 이렇게 선형적으로 모델을 만들어 보도록 하겠습니다.
선형이라는 단어는 '예측가능'이라는 의미를 내포하고 있습니다 ㅎㅎ
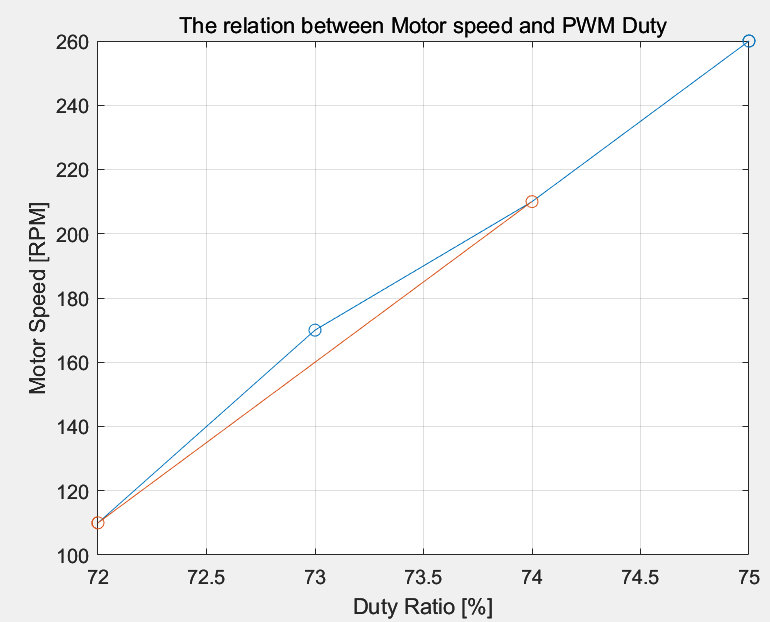
그런데 저 파랑색(실제 모터 응답)
빨강색(모델 응답)이
거의 비슷하지요?
그리고 우리는 저 빨강색 모델을을 1차 전달함수로 만들었습니다.
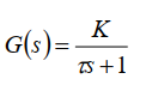
그리고, K의 값을 찾았는데
그 과정에서 Matlab을 어떻게 활용하였는지 정리해 보도록 하겠습니다.
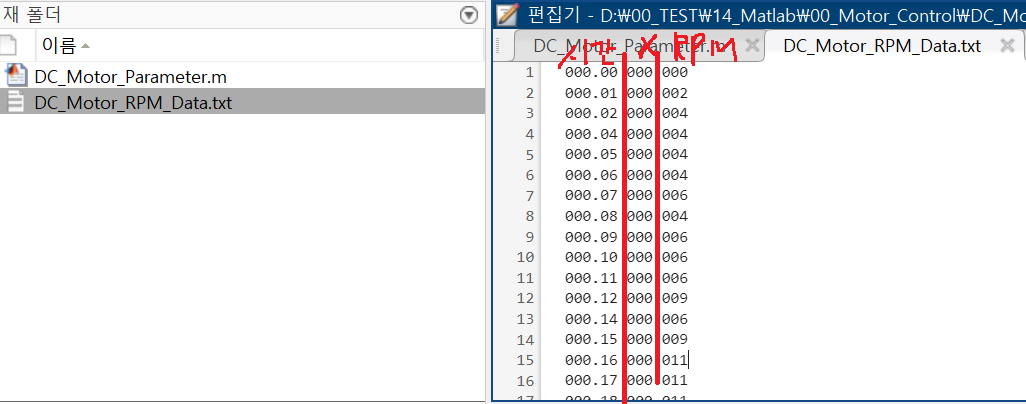
지금 DC_Motor_RPM_Data는
Duty에 따라서 RPM을 시간단위로 측정한 결과입니다.
이제 이 데이터를 Matlab으로 가지고 와야 합니다.
이때 importfile1 이라는
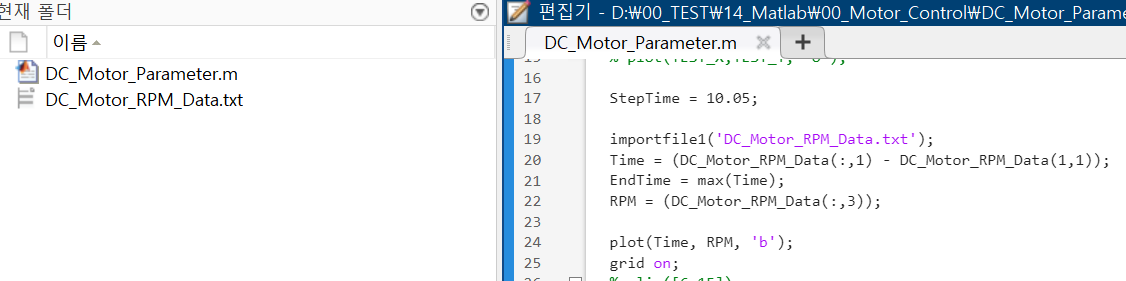
Matlab으로 수시을 표현하면 다음과 같습니다.
importfile1('DC_Motor_RPM_Data.txt');
Time = (DC_Motor_RPM_Data(:,1) - DC_Motor_RPM_Data(1,1));
EndTime = max(Time);
RPM = (DC_Motor_RPM_Data(:,3));
plot(Time, RPM, 'b');
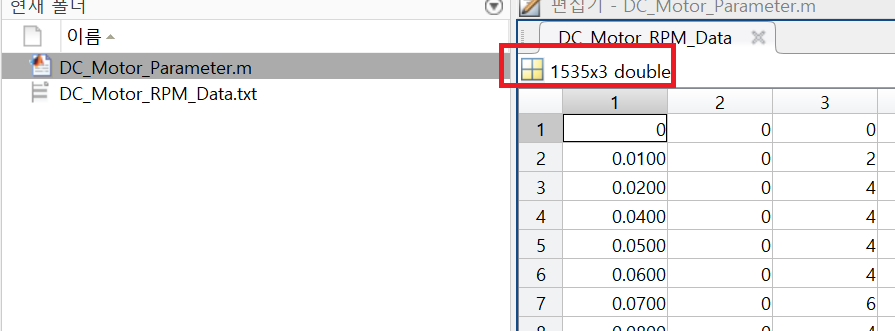
grid on;그러면 아래와 같이 데이터를 가지고 오게 됩니다.
3개의 열로 나오고 있는것을 볼 수 있습니다.
그리고 1열의 데이터를 Time으로
3열의 데이터를 RPM으로 가지고 오고 있는것을 확인할 수 있습니다.
그리고 획득한 데이터를 Matlab으로 그림을 그리면 아래와 같이 나오게 됩니다.
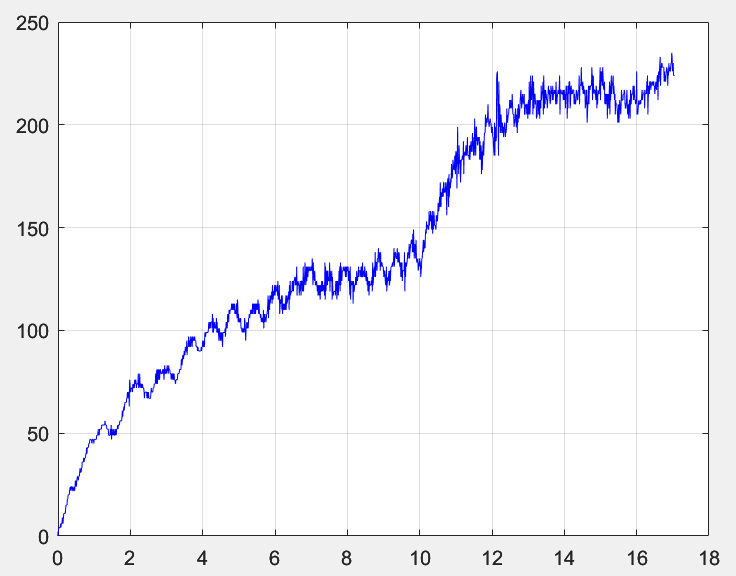
여기서 우리가 관심이 있어하는 부분은
Duty 72에서 Duty 74로 변경하는 부분입니다.
따라서 아래와 같이 6초 이후의 데이터만 필요합니다.
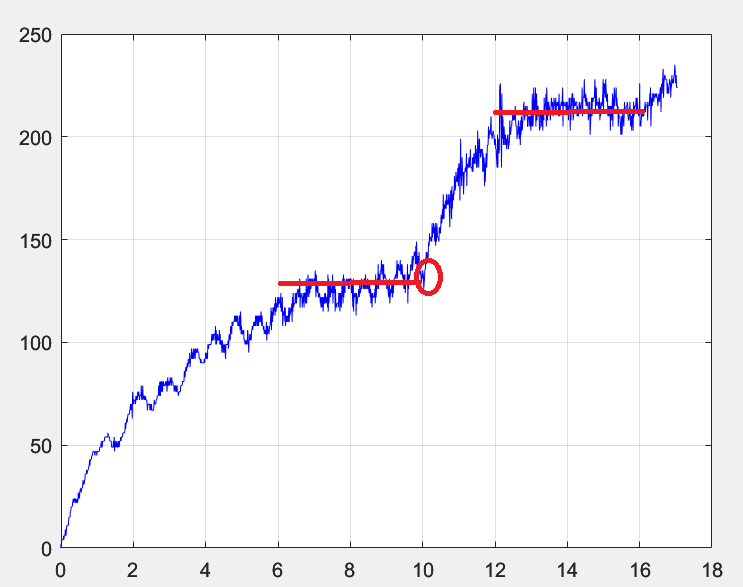
코드를 조금 수정해 보도록 하겠습니다.
이제 우리가 조금 보기 쉬운 그래프가 되었습니다.
importfile1('DC_Motor_RPM_Data.txt');
Time = (DC_Motor_RPM_Data(:,1) - DC_Motor_RPM_Data(1,1));
EndTime = max(Time);
RPM = (DC_Motor_RPM_Data(:,3));
plot(Time, RPM, 'b');
grid on;
xlim([6 15]);
title('DC Motor Speed');
xlabel('Time [s]');
ylabel('Motor Speed [RPM]');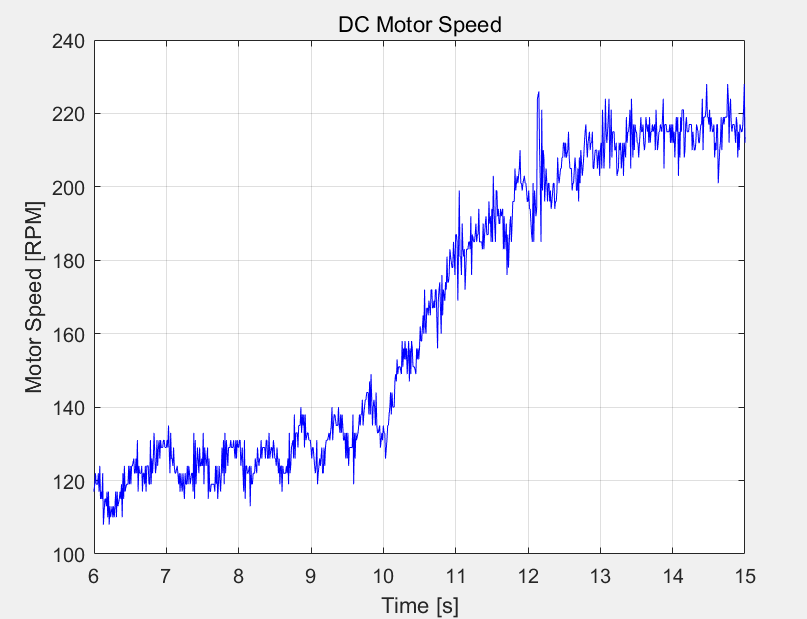
이제 K값을 구하려고 합니다.

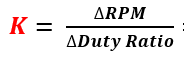
아래와 같이 2 부분에 대한 평균값이 필요합니다.
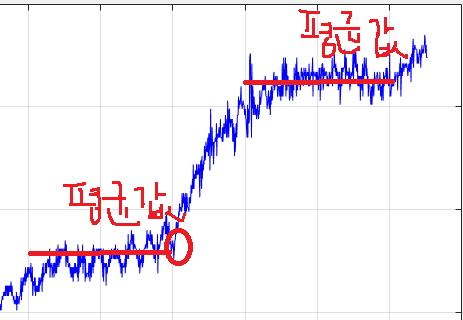
따라서 아래와 같은 데이터 처리가 필요합니다.
DutyChange = 74 - 72;
MeanStart = mean(RPM(541:905));
MeanEnd = mean(RPM(1188:1351));
K = ((MeanEnd - MeanStart) /(DutyChange));RPM 데이터 중에 541번 부터 905번까지는 아래 데이터를 나타냅니다.
따라서 이것의 평균값을 취하기 위하여 mean 함수를 사용하였습니다.
RPM 데이터의 1188부터 1351까지는 위의 라인 데이터입니다.
따라서 이것도 mean 함수를 사용하여 데이터를 획득합니다.
K를 구하는 수식을 통해 최종적으로 K값을 획득합니다.
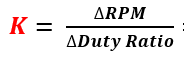
이렇게 해서 K가 44.32가 나오는 것을 알 수 있습니다.
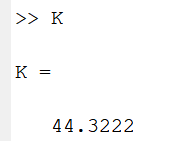
이제 Tau를 구하는 내용을 매트랩으로 조금더 정리해 보도록 하겠습니다.
Tau를 구하기 위해서는
먼저 RPM1에서 RPM2로 변화하는 과정에서 63%변하는 지점의 RPM값을 먼저 알아야 합니다.
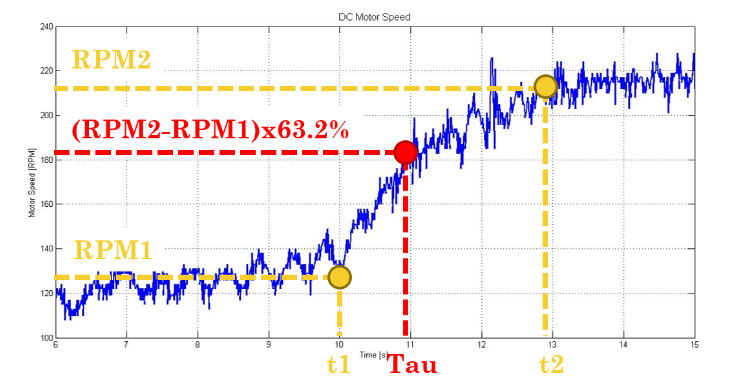
그래서 아래와 같은 수식이 필요합니다.
먼저 TauRPM을 구합니다.
TauRPM = (MeanEnd - MeanStart) * 0.632 + MeanStart;
DataLength = length(RPM);
TauRPM = (MeanEnd - MeanStart) * 0.632 + MeanStart;
flag = 0;
for i = 1:DataLength-1
if ( (RPM(i,1) < TauRPM) && (RPM(i+1,1) > TauRPM) && (flag == 0) )
Tau = (TauRPM - RPM(i,1)) * (Time(i+1,1) - Time(i,1) ) / (RPM(i+1,1) - RPM(i,1)) - StepTime + Time(i,1);
flag = 1;
end
endmatlab의 for 구문을 사용하여 구합니다.
c언어의 형식과 많이 비슷하지요?
1부터 쭉 확인하면서
TauRPM이 그 사이에 있을때까지 찾는 부분입니다.
그리고 RPMi와 RPMi+1 사이에 들어오게 되면
Tau값을 계산합니다.
아래와 같이 계산이 되는 것이지요!!
tau = (182.248 - 176) * (0.01) / (183 - 176) + 10.91 - 10.05
tau = 6.248 * 0.01 /7+ 10.91 - 10.05
tau = 0.86
이렇게 계속 한번 따라가는 이유는
매트랩이 행렬기반의 연산이라는 것을 한번 다시 확인하기 위해서 입니다.
아무리 복잡한 코드도 행렬기반의 연산이기 때문에
잘 보면 쉽게 이해될수 있습니다.
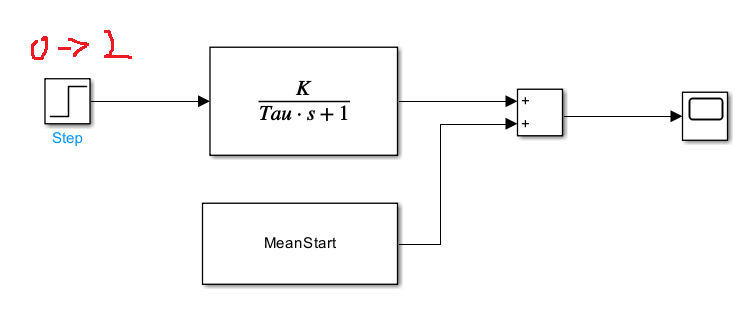
그렇다면 이제 한번 Matlab Simulink를 이용해서 DC 모터 모델링을 해보겠습니다.
Step은 0에서 2로 변경해 보겠습니다.
duty가 2% 변했기 때문입니다.
MeanStart는 126.1726 입니다.
그러면 그래프는 아래와 같이 그려지게 됩니다.
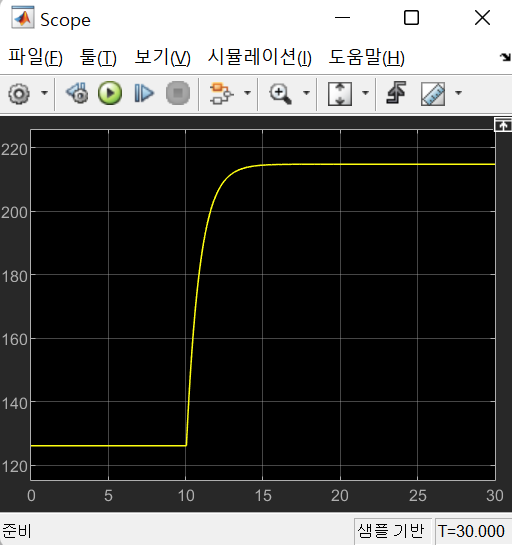
그러면 만든 모델이 실제 데이터와 얼마나 흡사한지를 확인하기 위해 데이터를 매트랩으로 가지고 오도록 하겠습니다.
아래와 같이 설저을 누르고 기록을 누르고
데이터를 workspace로 가져와 보도록 하겠습니다.
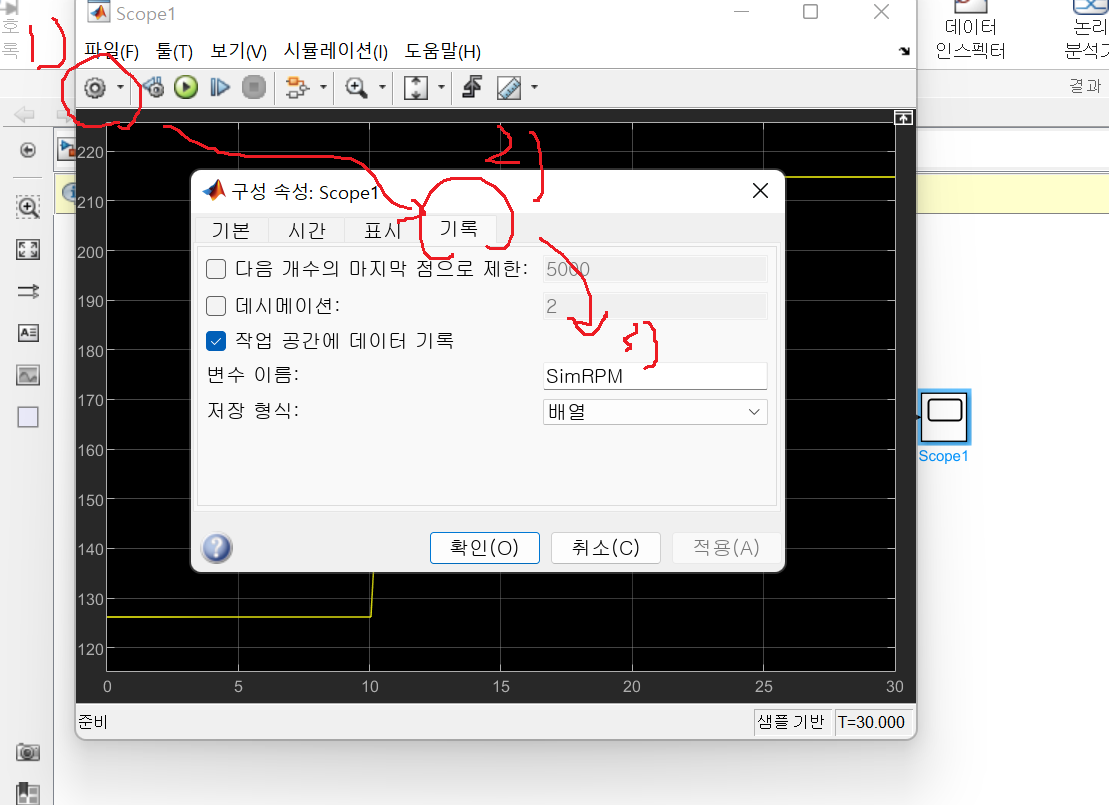
그리고 이제 모델을 열고
실행시켜서
데이터를 workspace로 가져오고
그림을 그리는 m 파일을 한번 만들어 보겠습니다.
% DCMotorModeling.mdl 파일 읽음
sim('DCMotorModeling.mdl');
hold on;
plot(SimRPM(:,1), SimRPM(:,2), 'r');
xlim([6 15]);
ylim([100 240]);
title('DC Motor Speed');
xlabel('Time [s]');
ylabel('Motor Speed [RPM]');
grid on;
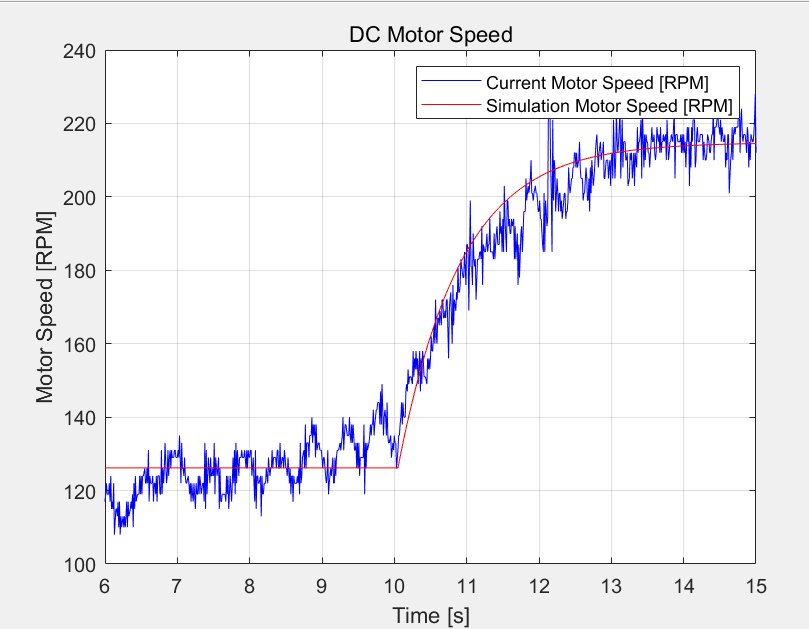
legend('Current Motor Speed [RPM]', 'Simulation Motor Speed [RPM]');이제 다 만들었습니다.
그러면 아래와 같이 실제 데이터와
모델이 비슷하게 동작하는 것을 볼 수 있습니다.
우리가 만든 모델이 이제 꽤 쓸모가 있는것 같습니다.
지금까지 수행한 내용은
아래와 같이 파일을 upload합니다.
이상으로 모터 모델링 관련 매트랩 사용법 정리 및 DC모터 시뮬레이션 글을 마치도록 하겠습니다.
'Embedded SW > Control Theory' 카테고리의 다른 글
| Pole이란 무엇이고, 1차 전달함수에서 Pole에 위치에 따른 응답특성은? (0) | 2022.09.26 |
|---|---|
| Feedback Controller 설계 방법 정리 (ex DC모터 제어, P Controller) (0) | 2022.09.26 |
| DAQ? Data Acquisition? DC모터 전달함수의 K와 Tau 값을 계산, 확인하는 방법 정리 (0) | 2022.09.24 |
| Simulink를 이용한 전달함수 시뮬레이션 수행 방법 정리 (0) | 2022.09.22 |
| DC모터 모델링, 매트랩 전달함수 생성 후 그래프 확인 (0) | 2022.09.21 |




댓글