반응형
안녕하세요.
오늘은 자료구조의 가장 첫부분에 있는 알고리즘 성능 분석에 대해서 글을 써보도록 하겠습니다.
이 자료는 예전 윤성우의 자료구조 부분을 공부하면서 정리한 내용입니다.
우리는 아래 그래프를 잘 알고 있습니다.
왼쪽은 지수식, 오른쪽은 로그식 그래프입니다.

여기서 x는 데이터의 수, 그리고 y는 쉽게 시간을 의미한다고 생각해 보겠습니다.
흠, 지수식 같은 경우, 데이터의 수가 늘어날 수록 처리 시간이 늘어나고 있습니다.
하지만 로그식 패턴의 알고리즘은, 데이터가 늘어나도 처리시간은 수렴된 다는 것을 알 수 있습니다.
그리고 이러한 알고리즘은 좋은 알고리즘이라고 할 수 있습니다.

알고리즘은 평가하는 요소는 두가지입니다.
1) 시간 복잡도 => 얼마나 빠른가? CPU에게 얼마나 부담을 주는가?
2) 공간 복잡도 => 메모리를 얼마나 많이 쓰느냐?
그러면 시간 복잡도가 더 중요할까요? 공간 복잡도가 더 중요할까요?
상황에 따라 다르지만, 메모리가 여유가 있을 경우에는
보통 시간 복잡도를 더 중요시 여깁니다.
시간의 복잡도는 연산의 횟수를 세어서 평가합니다.
데이터의 수에 대한 연산횟수를 함수로 만들게 되면 그래프로 그릴 수 있습니다.

데이터의 수가 적은 경우의 수행 속도는 큰 의미가 없습니다.
하지만 두 알고리즘 평가 기준은 데이터의 수가 늘어날때 얼마만큼의 연산 횟수가 증가하는가 입니다.

int LSearch(int ar[]. int len, int target)
{
int i;
for(i=0;i<len;i++)
{
if(ar[i] == target)
return i;
}
return -1;
}이것이 바로 순차 탐색 알고리즘 이라고 합니다.
배열의 주소, 길이, 그리고 찾고자 하는 인자를 정의하고 있습니다.
배열의 첫번째 부터 마지막까지 비교연산을 해서 그 인덱스를 반환하는 함수입니다.
위의 시간복잡도를 결정할 연산자는 무엇일까까요?
즉 == 입니다.
중심이 되는 연산자는 주변 연산자의 연산횟수에 영향을 미치게 됩니다.

바로 앞에 있을 경우에는 한번만 하면 됩니다.
T(n) = 1 best case
하지만 운이 나쁠 경우에는 가장 마지막에 들어 있게 됩니다.
즉, 배열이 n일 경우에 n번이 됩니다.
T(n) = n worst case
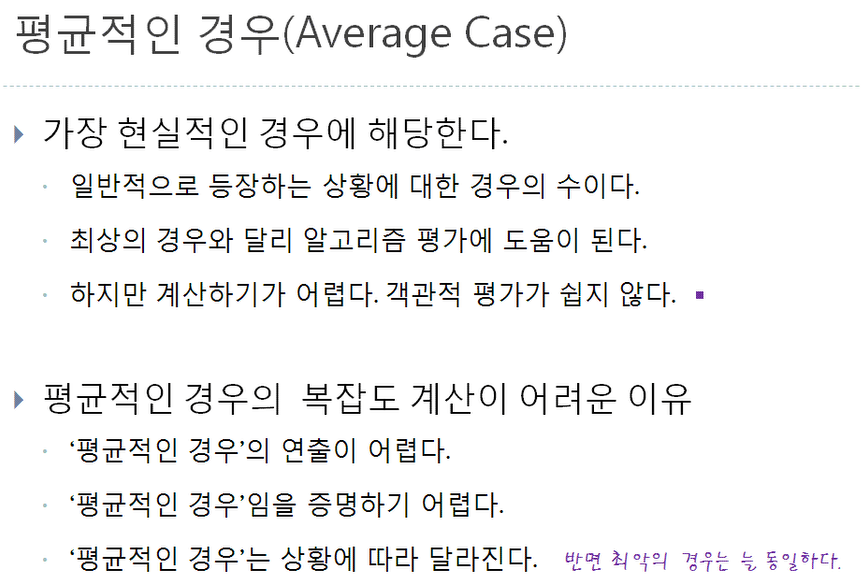
평균적인 경우는 상황에 따라 달라지고, 어렵다.
이것을 증명하기도 어렵지만
최악의 경우는 늘 동일합니다!!

따라서 순차 탐색의 최악의 경우 시간 복잡도는 T(n) = n 입니다.

아무튼 이렇게 열심히 계산했는데, 이것이 평균적이라는 근거를 이야기 하기가 쉽지 않네요.
다시 말해서, 평균적 경우로 생각하기 어렵습니다.
그러면 이제 이진 탐색 알고리즘을 한번 알아 보도록 하겠습니다.

이진 탐색 알고리즘의 전제는 배열이 정렬되어 있어야 한다는 점입니다.
위의 배열은 오름 차순으로 되어져 있습니다.
생각해 보자 우선 배열의 길이는 9입니다.
탐색의 시작위치는 index 0
마지막 위치는 index 8입니다.
(0+8)/2 = 4 이다.
그리고 index 4에 저장되어진 값과 3을 확인합니다.
그리고 나는 왼쪽으로 찾아야 할까요? 오른쪽으로 찾아야 할까요?
9이 3보다 크기 때문에 왼쪽으로 가야합니다.
즉, 9개의 탐색 대상이 4개로 줄었습니다.

0과 3을 더한다. 그리고 2로 나눕니다.
(0+3)/2 = 1 (나머지는 버린다)
흠 index 1을 보니 2이네요.
3보다 작으니까
오른쪽으로 움직여야 합니다.

(2+3)/2 = 2
arr[2]=3 우리가 찾은 3인것을 확인하였습니다.
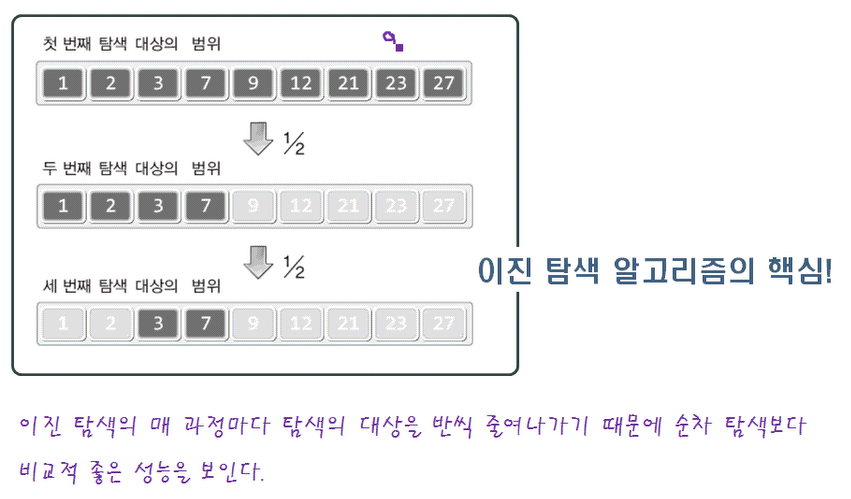
9->4->2으로 줄기 때문에 성능이 좋습니다.

while(first <= last)
{
}
만일 first > last가 되면 빠져나와야 합니다.
이럴때 탐색 타겟을 찾지 못했다고 생각할 수 있습니다.
1) 먼저(f+l)/2 = 중앙 index
2) 중앙 index의 배열값과 Target값의 비교
3) 왼쪽으로 갈 것인가? 오른쪽으로 갈 것인가?
int Bserch(int ar[]. int len, int target)
{
int first = 0;
int laft = len-1;
int mid;
while(first <= last)
{
mid =(first+last)/2;
if(target == ar[mid])
{
return mid; //탐색 완료!
}
else
{
if(target< ar[mid])
last = mid - 1; //오른쪽을 버리겠다.
else
first = mid + 1; //왼쪽을 버리겠다.
}
return -1; //찾지 못했을 때 반환되는 값 -1
}
핵심 연산자는 Targer == ar[mid]
이것이 핵심 연산자이다. 나머지 연산자는 저 핵심 연산자에 따라서 실행 횟수가 결정됩니다.
그렇다면 최악의 경우에 몇 번이 진행 될 것인가?
n개 == 1번
n/2 == 1번
n/4 == 1번
n/8 == 1번
..
1 == 1번

몇번에 대해서 == 비교 연산자를 수행하는지는 알기가 어렵습니다.

생각을 해보자!
123456789 => 총 9개라고 치면
12345 => 5
1234 => 2
34=>
1


결국 최악에 대한 시간 복잡도 함수는 위와 같습니다.
이제 빅오 표기법을 마무리로 알고리즘 분석을 마치도록 하겠습니다.
한번 생각을 해보겠습니다.
T(n) = n2 + 3 => n2로 생각할수 있습니다.
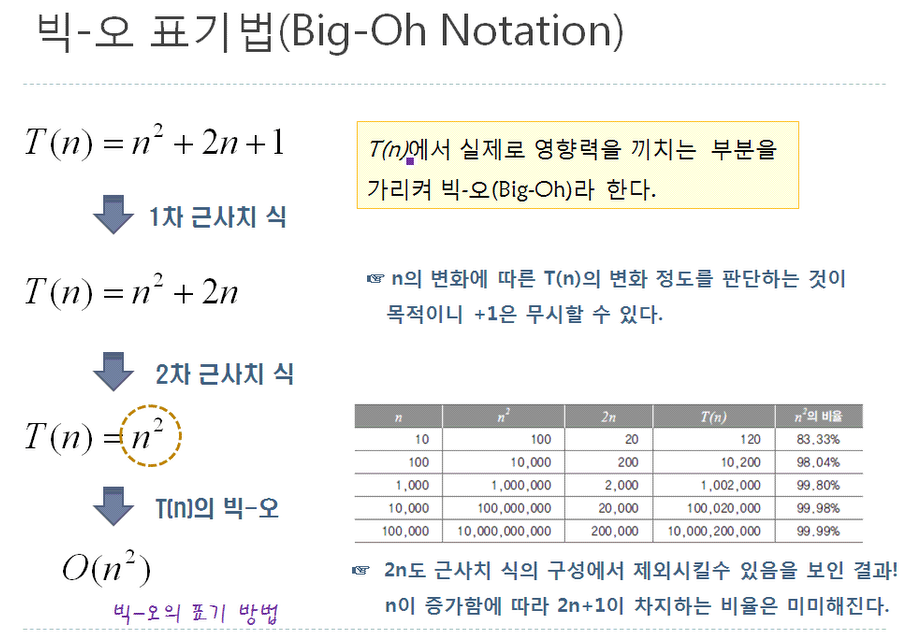
빅오라는 것은 T(n)에서 실제 영향력을 끼치는 부분을 의미합니다.


상수형 비고가 의미하는 것은 무엇일까요?
n이 무엇이든지간에 연산횟수는 정해져 있다는 것입니다.
보통 로그형 빅-오를 보이는 알고리즘이 좋은 알고리즘이라고 할 수 있습니다.
정리하면 아래와 같습니다.

인진 탐색 알고리즘이 n이 많아질 수록 확실히 연산횟수가 적음을 확인 할 수 있습니다.

이것으로 알고리즘 성능 분석 방법 정리 (순차탐색알고리즘, 이진탐색알고리즘 비교)를 마치도록 하겠습니다.
반응형
'Computer Language > Data Structure' 카테고리의 다른 글
| [자료구조] 05. Queue List 구조 예제 (C언어) (0) | 2021.07.10 |
|---|---|
| [자료구조] 04. Queue 배열 구조 예제 (C언어) (0) | 2021.07.10 |
| [자료구조] 03. Stack Flood Fill 예제 (C언어) (0) | 2021.07.10 |
| [자료구조] 02. Stack 구조 Basic 예제 (C언어) (0) | 2021.07.09 |
| [자료구조] 01. List 구조 Baisc 예제 (C언어) (0) | 2021.07.09 |




댓글